
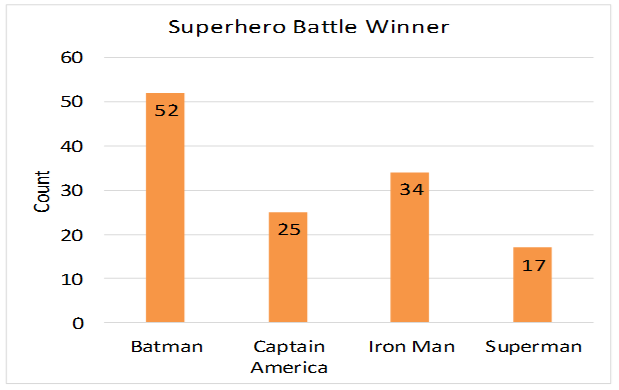
Since a coin has two sides, it has 50% chance of landing on tail. The cumulative frequency is calculated by adding each frequency from a frequency distribution table to the sum of its predecessors. It is also said as temporal frequency. It is also referred to as temporal frequency. In Statistics, Frequency is defined as the number of occurrences of a repeating event per unit of time. Frequency Chart Generator.
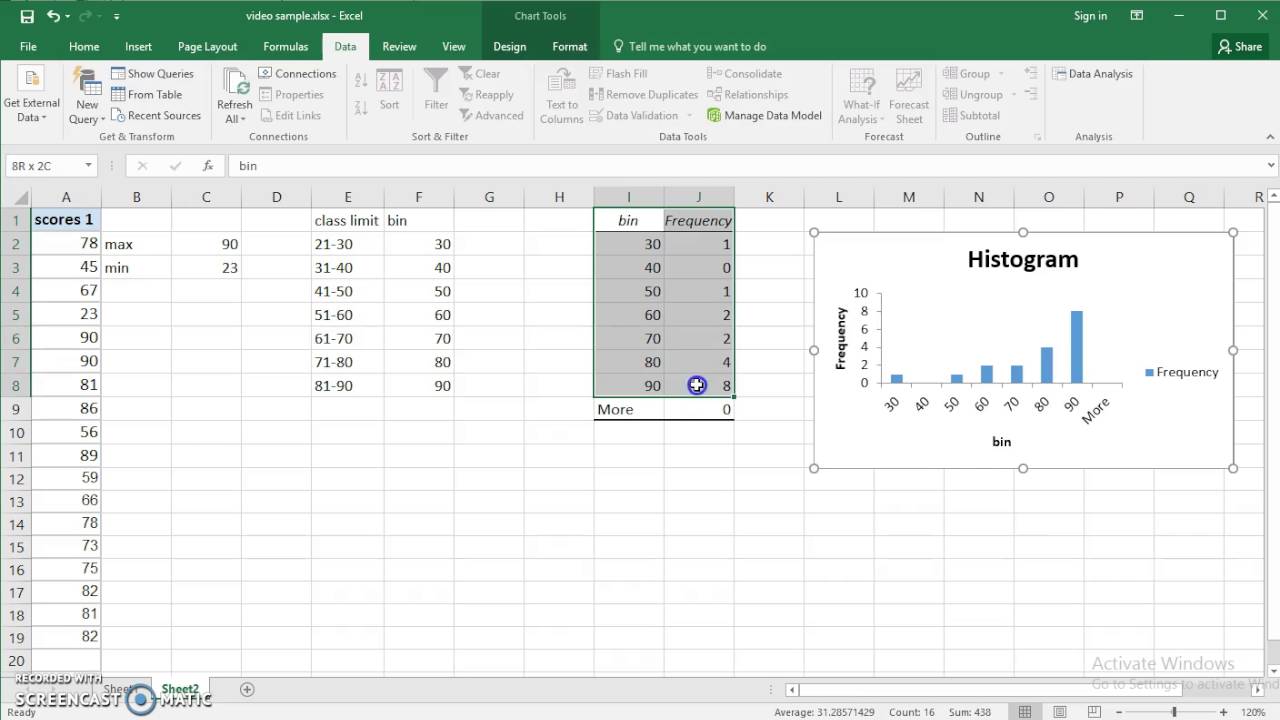
Frequency Table To Histogram Free Online Math
Maphimbu also works with floating point: jot -r 100.0 10 15 numprocess /10/ maphimbu -s 1.Instructions: Use our histogram maker to provide the data fore which you want. Output: 1 20 2 21 3 20 4 21 5 18. Using maphimbu from the Debian stda package: use 'jot' to generate 100 random numbers between 1 and 5 and 'maphimbu' to print sorted 'histogram': jot -r 100 1 5 maphimbu -s 1. Search The Best Law at Law Details: It is also said as temporal frequency.The cumulative frequency is calculated by adding each frequency from a frequency distribution table to the sum of its predecessors.2. The first and the third question are not easy to answer since they may require a solid understanding of the topic and some contextual information.Frequency Chart Generator - Free Online Math Calculator.
Following the steps below to create a frequency table and histogram. To compute the probability of exactly 8 successes, select Calc > Probability Distributions > Binomial.Once the Data Analysis Toolpak is installed, you can create a frequency table. I need to calculate the odds for a binomial distribution with 10 trials (n=10) and probability of success p=0.5. Suppose I want to know the probability of getting a certain number of heads in 10 tosses of a fair coin.
As atmost one means not more than one which we can say it can be zero also. Therefore the probability of getting atmost one head can be. Sampling from two probability distributions - quantitative Classics (j) Histogram Bin Width Dotplot Summaries Sampling Pennies Sampling Change Sampling 2005 Senators Friendly Observers Dolphin Study applet Yawning Study applet Two-way Table simulation applet Randomization Test for quantitative response (two groups) (f) The stats record also has a new array to hold 'repeat counts', but this will be. Step 1: Decide how many classes you want in the frequency table.Update September 2018: To create a frequency histogram in 12c the cumulative frequency has to be 2,050 or greater.
So, P( at least one head)=1-1/64=63/64. The P(No heads)=(1/2)^6=1/64. The probability is 1- P( No heads). Why the date of the places named are not same?ls the date the same in all the places named on the map?(ii) Explain your answer.Please answer both
The “Historical Probability of a White Christmas” map shows the climatological probability of at least 1 inch of snow being on the ground on December 25 in the contiguous United States. For example, if we flip a coin many, many times, we expect to see half the flips turn up heads , but only in the long run. If an event occurs x times out of n, then its probability will converge on x ÷ n as n becomes infinitely large. The probability of an event is its relative frequency (expected proportion) in the long run.
(HH, HT, TH, TT} Favourable outcomes are 3, i.e. Solution: Total outcomes are 4, i.e. Find the probability of getting at least one head. A coin is tossed two times.
" P(2 heads) = 1/4 = 0.25 We MUST get either 0, or 1, or 2 heads on the toss. " P(0 heads) = 1/4 = 0.25 ! Probability of getting 2 head. " P(1 head) = 2/4 = 0.50 ! Probability of getting 0 heads.
Since the sample size n appears in the denominator of the square root, the standard deviation does decrease as sample size increases. The result might have been expected: 1/2 is the probability of the heads on a single toss. Since each contains 4 outcomes out of the equiprobable 8, P(A) = P(B) = 4/8 = 1/2. B is the event in which heads came up on the second toss. How about the probability of getting AT LEAST 5 heads in 10 coin tosses? A is the sequence of tosses in which the third one came up heads.
Since the coin is fair, the two outcomes (“heads” and “tails”) are both equally probable the probability of “heads” equals the probability of “tails” and since no other outcomes are possible, the probability of either “heads” or “tails” is 1/2 (which could also be written as 0.5 or 50%). The point is not the rarity of a 51st toss of heads, but the improbability of that 51st toss being preceded by 50 heads in a row. The probability that the 51st toss of a fair coin will be heads is indeed 1/2, However, the chance of all 51 tosses being heads is 1 in 2^51, which is a very small chance indeed. The convention is to require both np and n(1 – p) to be at least 10.


 0 kommentar(er)
0 kommentar(er)
